3.2 2D and 3D Delaunay TriangulationThe Delaunay triangulation and the Voronoi diagram are dual structures and contain the same information in different form. Computing one of these structures does automatically create the other. Furthermore there is a connection between Delaunay triangulations and convex hulls in one higher dimension. The Delaunay triangulation and the Voronoi diagram in d dimensions can be constructed from a convex hull in d+1 dimensions. The Delaunay triangulation for a set of d-dimensional points is the projection of the points of the hull in d+1 dimensions. A introduction can be found in [ ORo98 ]. • 2D Delaunay Triangulation Two algorithmic variants of the 2D Delaunay triangulation have been implemented. One is the incremental algorithm [ Lis94 ] and the other the recursive variant with a ''divide and conquer'' strategy [ GSt85 ]. The two following images show the Delaunay triangulation (Figure 4a) and the corresponding Voronoi diagram (Figure 4b), created from 5964 points.
Figure 5 shows both, the Delaunay triangulation and the Voronoi diagram, in one image, for a set of 10 points. 
• Voronoi Diagram on the Sphere Figure 6 shows a Voronoi diagram, created from the positions of the capitals of 228 countries (including overseas territories and the like) blended with the world map. The red dots show the GPS positions of the capitals, which have been transformed to 3D points using the WGS-84 [ WGS84 ] ellipsoid. The diagram has been created from the convex hull of these points. The following WebGL link shows a 3D model of this Voronoi diagram: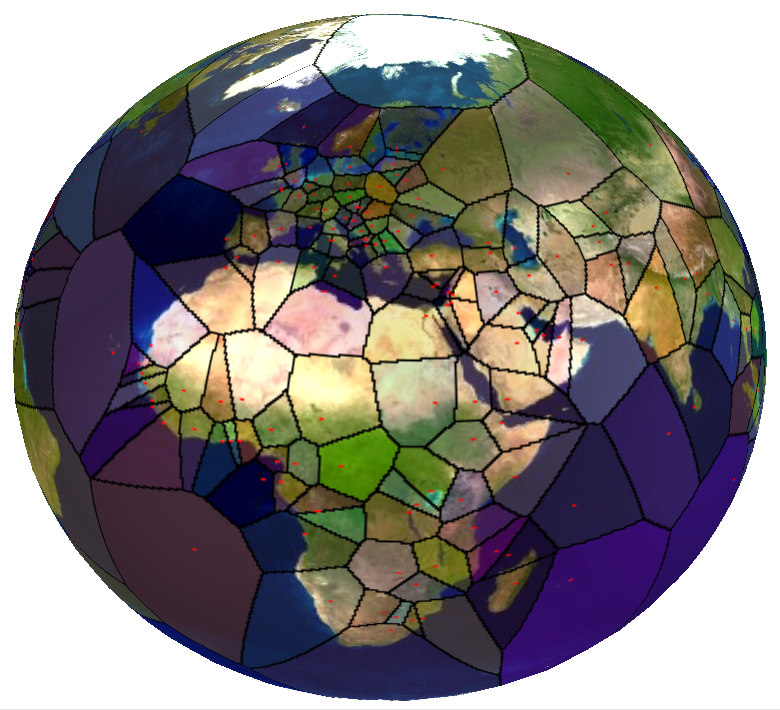 
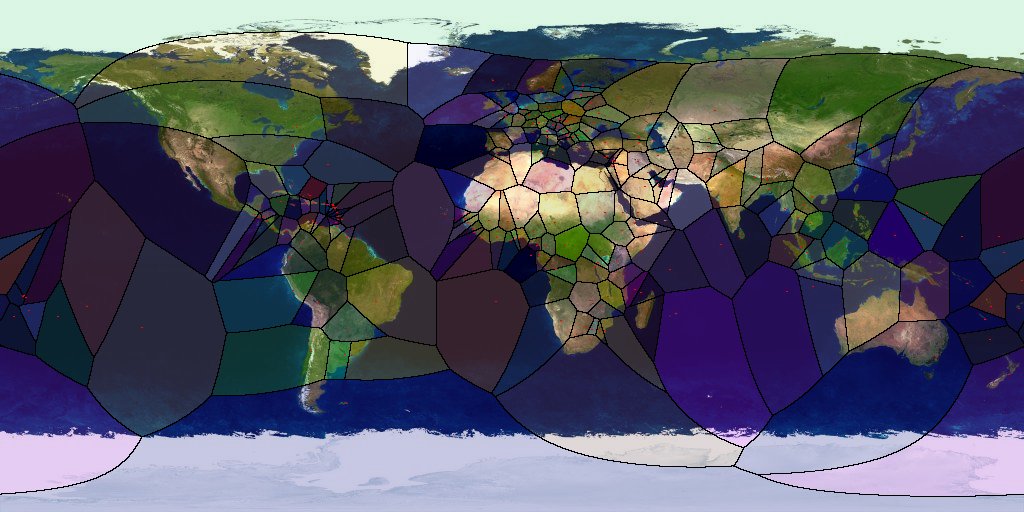
. Figure
7 shows this Voronoi diagram of the whole world in 2D.
• 3D Delaunay Triangulation The implementation of the 3D Delaunay triangulation is based on the algorithm described in [ ESh96 ]. An extensive description (in German) can be found in [ BKl06 ]. The following two images (Figure 8a and Figure 8b) show the well known Stanford Bunny. The right one shows a 3D Delaunay triangulation of 71 weighted points of its point set.
The 3D Delaunay triangulation for point sets with symmetries can be generated with the help of Simulation of Simplicity [ EMu90 ]. The following two images (Figure 9a and Figure 9b) show an icosahedron. The right Figure 9b shows a possible 3D Delaunay triangulation of this platonic solid.
The following WebGL links show 3D models of the 3D Delaunay triangulations: Bunny
and Icosahedron
.
|
